Day 28 Crossover Designs II
July 22nd, 2025
28.1 Announcements
- Project due on Wednesday to send for peer review.
- The Difference Between “Significant” and “Not Significant” is not Itself Statistically Significant - Gelman and Stern (2012)
- Homework due tomorrow, 7am: write a question in this Google Docs, or answer a question someone made. Make sure you have your track changes on, or leave your last name in a comment.
28.2 Crossover designs
Baseline:
- Apply treatments to the same experimental unit sequentially, to eliminate between-experimental unit variation when comparing treatments
- Fewer EUs (probably living beings) are required than in non-crossover designs
- Power (?)
- Between-EU variability is accounted for in the model
- Sources of variability:
- Treatment ( \(\geq\) 2)
- Period ( \(\geq\) 2)
- Sequence ( \(\geq\) 2)
- Carryover (residual) effects
- Between-individuals
- The EUs are randomized to sequences
- What is the difference between crossover designs capturing between-individuals variability, and subsampling?
Overall model:
\[y_{ijklm} = \mu + T_i + P_j + S_k +C_{l} + u_m + \varepsilon_{ijklm}, \\ u_{m} \sim N(0, \sigma^2_u), \\ \varepsilon_{ijklm} \sim N(0, \sigma^2_\varepsilon),\] where:
- \(y_{ijk}\) is the observation for the \(i\)th treatment, \(j\)th period with the \(m\)th previous treatment and the \(m\)th individual that received the treatments in the \(k\)th sequence,
- \(T_i\) is the effect of the \(i\)th treatment,
- \(P_j\) is the effect of the \(j\)th period,
- \(S_k\) is the effect of the \(k\)th sequence,
- \(C_{l}\) is the carryover effect of the \(l\)th treatment,
- \(u_{mk}\) is the (random) effect of the \(m\)th individual under the \(k\)th sequence, and \(\varepsilon_{ijkl}\) is the residual.
Considerations:
Carryover effects:
- Experiment designs may be better or worsely designed to separate carryover effect from treatment effect.
- Type of treatment, adequate time between treatments (“wash out” period)
- Some treatments may damage the individual for indefinite time (e.g., damaging the liver)
Repeated measures:
- When \(P > 2\), the several measurements on the same individual assume a compound symmetry correlation function.
- Other types of correlation functions assume that the correlation “wears out” with time (e.g., AR(1) correlation function)
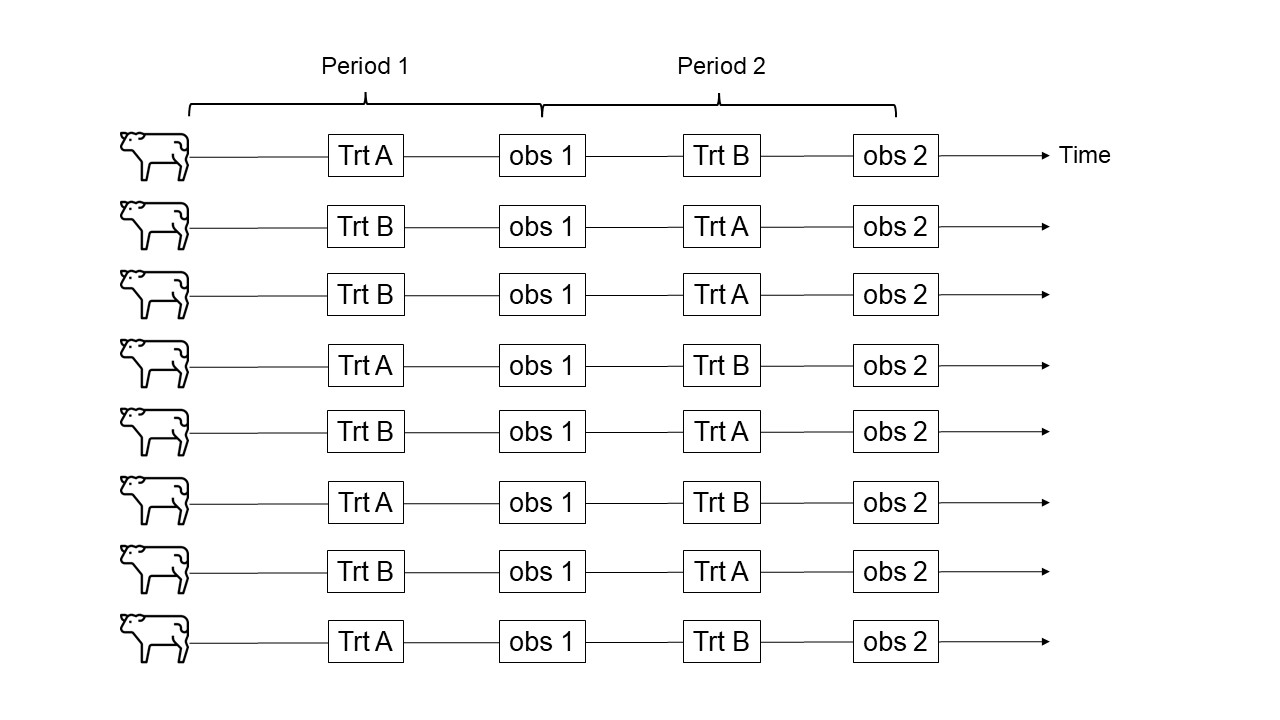
Figure 28.1: Schematic representation of a 2x2 crossover design
28.3 Applied example
6 cows were used to test 3 different treatments in a crossover design.
- Repeated measures. Now we are assuming compound symmetry (a specific type of correlation function).
- How does carryover affect power?
url <- "https://raw.githubusercontent.com/stat720/summer2025/refs/heads/main/data/cow_prod_cox.csv"
df <- read.csv(url)
df## Cow Sequence Period Treatment Prior_trt milk_production
## 1 1 ABC 1 A O 38
## 2 1 ABC 2 B A 25
## 3 1 ABC 3 C B 15
## 4 2 BCA 1 B O 109
## 5 2 BCA 2 C B 86
## 6 2 BCA 3 A C 39
## 7 3 CAB 1 C O 124
## 8 3 CAB 2 A C 72
## 9 3 CAB 3 B A 27
## 10 4 ACB 1 A O 86
## 11 4 ACB 2 C A 76
## 12 4 ACB 3 B C 46
## 13 5 BAC 1 B O 75
## 14 5 BAC 2 A B 35
## 15 5 BAC 3 C A 34
## 16 6 CBA 1 C O 101
## 17 6 CBA 2 B C 63
## 18 6 CBA 3 A B 1library(lme4)
library(emmeans)
m_milk.nocarryover <- lmer(milk_production ~ Sequence + Period + Treatment + (1|Sequence:Cow),
data = df)
emmeans(m_milk.nocarryover, ~ Treatment )## Treatment emmean SE df lower.CL upper.CL
## A 45.2 4.65 17.6 35.4 54.9
## B 57.5 4.65 17.6 47.7 67.3
## C 72.7 4.65 17.6 62.9 82.4
##
## Results are averaged over the levels of: Sequence
## Degrees-of-freedom method: kenward-roger
## Confidence level used: 0.95m_milk.carryover <- lmer(milk_production ~ Sequence + Period + Treatment + Prior_trt + (1|Sequence:Cow),
data = df)
car::Anova(m_milk.carryover, test.statistic = "F")## Analysis of Deviance Table (Type II Wald F tests with Kenward-Roger df)
##
## Response: milk_production
## F Df Df.res Pr(>F)
## Sequence 10.8253 5 26.11 1.023e-05 ***
## Period 91.2965 1 6.00 7.504e-05 ***
## Treatment 41.1220 2 6.00 0.0003143 ***
## Prior_trt 6.0141 3 6.00 0.0306394 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Treatment emmean SE df lower.CL upper.CL
## A 42.8 3.05 10.6 36.0 49.5
## B 56.4 3.05 10.6 49.6 63.1
## C 77.0 3.05 10.6 70.3 83.7
##
## Results are averaged over the levels of: Sequence, Prior_trt
## Degrees-of-freedom method: kenward-roger
## Confidence level used: 0.95